Accounting and Conservation Equations
The Problem
The problem is writing code for personal accounting for a person with 4 accounts but receiving income on one only, and using all of them for payments and transfers. But first: understanding the physics.
The governing equation is,
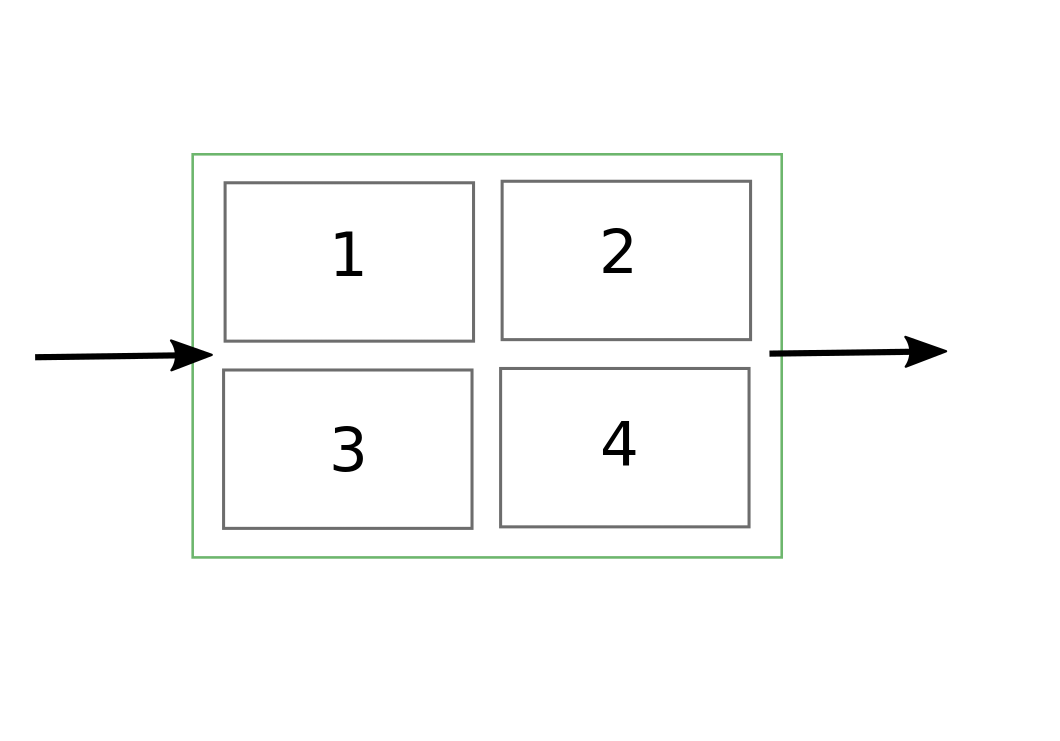
\[\Delta=\sum I-\sum L\]For \(I\) and \(L\) that cross the system boundary (in green below). \(I\) and \(L\) for accounts \(1\) through \(4\) are known as total in and out of each account, but not each stream. My goal is to calculate each term in this equation
\[\Delta = I_1-(L'_1+L_2+L'_3+L_4)\]to find \(\sum L\).
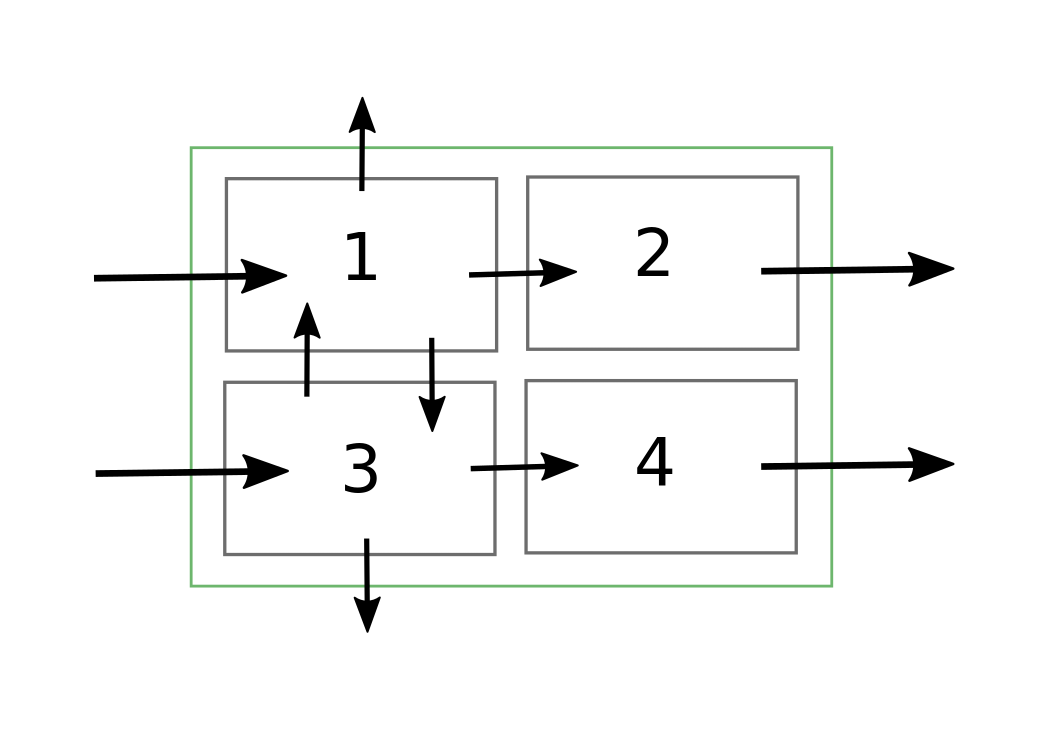
Notation
\(I_1\) is the total income for account \(1\).
\(I'_1\) is the part of the income for account \(1\) coming from the 1st stream.
\(L'''_2\) is the part of the loss for account \(2\) going to the 3rd stream. And so on.
Calculations
Method 1
For a single income account,
\[\sum I=I_1\]Money flows out in 3 directions out of the 1st account,
\[L_1=L'_1+L''_1+L'''_1\]\(L''_1\) and \(L'''_1\) are known quantities:
\[L_1=L'_1+I_2+I_3\]Money flows out in 2 directions out of the 3rd account,
\[L_3=L'_3+L''_3\]\(L''_3\) is a known quantity:
\[L_3=L'_3+I_4\]Therefore,
\[L'_1=L_1-(I_2+I_3)\]and
\[L'_3=L_3-I_4\]which can be substituted in the above equation to get \(\Delta\) and \(\sum L\).
Method 2
This approach is inspired by the conservation equations of physics:
\[\Delta=\Delta_1+\Delta_2+\Delta_3+\Delta_4\]where
\[\Delta_i=I_i-L_i\]Knowing the total income you can get the total losses by using the governing equation above. However, this appears confusing because it is a difference between larger numbers than the first method (because it accounts for the internal interactions between accounts), but it’s the same \(\Delta\). So,
\[L_{ext}=I_{ext}-\Delta\]where in this case
\[I_{ext}=I_1\]This phenomenon of flow is all over nature (e.g. calculating the change in internal energy and entropy of a system) and it has always confused me by its simplicity. I am writing this down to stop being confused by it!